Code
import numpy as np
import pandas as pdkakamana
April 9, 2023
In this chapter, you will be introduced to another popular automated hyperparameter tuning method known as Random Search. You will learn what it is, how it works, and how it differs from grid search. You will learn about the advantages and disadvantages of this method and when to choose it over Grid Search. In this lesson, you will practice conducting a Random Search using Scikit Learn, as well as visualizing and interpreting the results.
This Random Search is part of Datacamp course: Hyperparameter Tuning in Python Hyperparameters play a significant role in the development of powerful machine learning models. However, with increasingly complex models with numerous options available, how can you efficiently identify the best settings for your particular issue? You will gain practical experience using some common methodologies for automated hyperparameter tuning in Python using Scikit Learn. Among these are Grid Search, Random Search, and advanced optimization methodologies such as Bayesian and Genetic algorithms. To dramatically increase the efficiency and effectiveness of your machine learning model creation, you will use a dataset predicting credit card defaults.
This is my learning experience of data science through DataCamp. These repository contributions are part of my learning journey through my graduate program masters of applied data sciences (MADS) at University Of Michigan, DeepLearning.AI, Coursera & DataCamp. You can find my similar articles & more stories at my medium & LinkedIn profile. I am available at kaggle & github blogs & github repos. Thank you for your motivation, support & valuable feedback.
These include projects, coursework & notebook which I learned through my data science journey. They are created for reproducible & future reference purpose only. All source code, slides or screenshot are intellactual property of respective content authors. If you find these contents beneficial, kindly consider learning subscription from DeepLearning.AI Subscription, Coursera, DataCamp
To undertake a random search, we firstly need to undertake a random sampling of our hyperparameter space.
In this exercise, you will firstly create some lists of hyperparameters that can be zipped up to a list of lists. Then you will randomly sample hyperparameter combinations preparation for running a random search.
You will use just the hyperparameters learning_rate and min_samples_leaf of the GBM algorithm to keep the example illustrative and not overly complicated.
from itertools import product
from pprint import pprint
# Create a list of values for the learning_rate hyperparameter
learn_rate_list = list(np.linspace(0.01, 1.5, 200))
# Create a list of values for the min_samples_leaf hyperparameter
min_samples_list = list(range(10, 41))
# Combination list
combinations_list = [list(x) for x in product(learn_rate_list, min_samples_list)]
# Sample hyperparameter combinations for a randomsearch
random_combinations_index = np.random.choice(range(0, len(combinations_list)),
30, replace=False)
combinations_random_chosen = [combinations_list[x] for x in random_combinations_index]
# Print the result
pprint(combinations_random_chosen)[[0.9384422110552764, 17],
[0.8635678391959799, 18],
[0.7812060301507537, 31],
[1.4401005025125628, 14],
[0.3094974874371859, 10],
[1.4251256281407034, 19],
[1.3577386934673366, 14],
[1.4925125628140703, 10],
[0.9010050251256281, 35],
[0.796180904522613, 26],
[1.178040201005025, 22],
[0.5490954773869346, 26],
[1.095678391959799, 18],
[0.42180904522613066, 10],
[0.3768844221105528, 25],
[1.372713567839196, 36],
[1.095678391959799, 22],
[1.0058291457286432, 13],
[0.06241206030150754, 40],
[0.6464321608040201, 25],
[0.5715577889447236, 32],
[0.4292964824120603, 27],
[0.5715577889447236, 17],
[1.1555778894472362, 34],
[1.1930150753768844, 35],
[0.017487437185929648, 24],
[0.5116582914572865, 13],
[0.2121608040201005, 12],
[0.668894472361809, 13],
[1.1106532663316582, 16]]To solidify your knowledge of random sampling, let’s try a similar exercise but using different hyperparameters and a different algorithm.
As before, create some lists of hyperparameters that can be zipped up to a list of lists. You will use the hyperparameters criterion, max_depth and max_features of the random forest algorithm. Then you will randomly sample hyperparameter combinations in preparation for running a random search.
import random
# Create lists for criterion and max_features
criterion_list = ['gini', 'entropy']
max_feature_list = ['auto', 'sqrt', 'log2', None]
# Create a list of values for the max_depth hyperparameter
max_depth_list = list(range(3, 56))
# Combination list
combinations_list = [list(x) for x in product(criterion_list, max_feature_list, max_depth_list)]
# Sample hyperparameter combinations for a random search
combinations_random_chosen = random.sample(combinations_list, 150)
# Print the result
print(combinations_random_chosen)[['gini', 'sqrt', 49], ['entropy', 'auto', 40], ['gini', 'auto', 53], ['gini', 'log2', 55], ['entropy', 'log2', 25], ['entropy', 'sqrt', 11], ['entropy', 'log2', 27], ['gini', 'log2', 22], ['entropy', 'auto', 21], ['gini', 'auto', 49], ['gini', 'auto', 31], ['entropy', None, 5], ['gini', 'sqrt', 20], ['entropy', 'auto', 25], ['entropy', 'auto', 24], ['entropy', 'sqrt', 42], ['gini', 'sqrt', 28], ['entropy', None, 40], ['entropy', None, 31], ['gini', 'sqrt', 55], ['entropy', 'sqrt', 26], ['gini', None, 29], ['gini', 'sqrt', 44], ['gini', 'sqrt', 26], ['entropy', None, 35], ['gini', 'auto', 47], ['gini', 'auto', 13], ['gini', None, 9], ['entropy', 'sqrt', 5], ['gini', 'log2', 47], ['gini', 'sqrt', 5], ['gini', 'log2', 36], ['entropy', 'log2', 55], ['gini', None, 24], ['gini', 'log2', 19], ['gini', 'auto', 7], ['entropy', None, 37], ['entropy', 'sqrt', 8], ['gini', None, 27], ['gini', 'auto', 24], ['gini', 'auto', 19], ['gini', 'log2', 44], ['gini', 'log2', 18], ['entropy', 'log2', 21], ['entropy', None, 43], ['gini', 'log2', 52], ['entropy', None, 18], ['entropy', 'sqrt', 23], ['gini', None, 55], ['entropy', 'auto', 18], ['gini', 'sqrt', 39], ['entropy', 'log2', 9], ['gini', None, 46], ['gini', 'sqrt', 36], ['gini', None, 34], ['gini', 'auto', 39], ['gini', 'sqrt', 9], ['entropy', 'log2', 3], ['entropy', 'log2', 16], ['entropy', 'auto', 5], ['entropy', 'sqrt', 38], ['entropy', None, 38], ['entropy', 'auto', 39], ['entropy', 'log2', 40], ['gini', None, 33], ['gini', None, 7], ['entropy', 'sqrt', 43], ['gini', None, 28], ['entropy', 'log2', 50], ['gini', 'sqrt', 48], ['gini', 'sqrt', 45], ['entropy', 'sqrt', 20], ['gini', 'sqrt', 13], ['entropy', 'auto', 51], ['entropy', 'auto', 42], ['gini', 'auto', 12], ['gini', 'log2', 8], ['gini', 'log2', 38], ['entropy', None, 20], ['entropy', 'auto', 7], ['entropy', 'auto', 41], ['gini', 'sqrt', 35], ['entropy', 'sqrt', 3], ['gini', None, 26], ['gini', 'log2', 17], ['entropy', None, 42], ['entropy', None, 15], ['gini', None, 43], ['entropy', 'sqrt', 35], ['entropy', 'sqrt', 31], ['entropy', 'sqrt', 6], ['entropy', None, 51], ['gini', None, 5], ['gini', 'auto', 8], ['gini', 'auto', 32], ['entropy', None, 33], ['gini', 'log2', 33], ['entropy', 'log2', 22], ['gini', 'sqrt', 31], ['gini', 'sqrt', 33], ['gini', 'log2', 7], ['gini', 'auto', 35], ['gini', 'log2', 40], ['entropy', None, 39], ['gini', 'auto', 36], ['entropy', None, 10], ['entropy', None, 6], ['gini', None, 41], ['gini', 'sqrt', 11], ['gini', 'log2', 14], ['entropy', 'auto', 48], ['gini', 'auto', 50], ['entropy', 'auto', 45], ['entropy', None, 44], ['entropy', 'log2', 24], ['gini', 'log2', 11], ['entropy', 'sqrt', 21], ['gini', 'sqrt', 7], ['gini', 'sqrt', 6], ['entropy', 'sqrt', 14], ['entropy', 'log2', 42], ['gini', 'log2', 41], ['entropy', 'auto', 34], ['entropy', 'sqrt', 15], ['gini', 'log2', 4], ['gini', 'sqrt', 52], ['gini', 'log2', 48], ['gini', None, 14], ['gini', 'sqrt', 3], ['gini', 'sqrt', 43], ['gini', 'sqrt', 19], ['gini', 'auto', 40], ['entropy', 'auto', 16], ['entropy', None, 29], ['gini', None, 52], ['entropy', 'sqrt', 29], ['entropy', 'log2', 44], ['entropy', 'auto', 53], ['entropy', 'auto', 36], ['gini', 'auto', 20], ['gini', 'log2', 39], ['gini', 'auto', 37], ['gini', 'auto', 45], ['gini', 'sqrt', 17], ['entropy', None, 28], ['gini', 'auto', 27], ['entropy', 'log2', 52], ['entropy', 'log2', 47], ['entropy', 'log2', 31], ['gini', 'sqrt', 34]]Visualizing the search space of random search allows you to easily see the coverage of this technique and therefore allows you to see the effect of your sampling on the search space.
In this exercise you will use several different samples of hyperparameter combinations and produce visualizations of the search space.
The function sample_and_visualize_hyperparameters() takes a single argument (number of combinations to sample) and then randomly samples hyperparameter combinations, just like you did in the last exercise! The function will then visualize the combinations.
import matplotlib.pyplot as plt
def sample_and_visualize_hyperparameters(n_samples):
# If asking for all combinations, just return the entire list.
if n_samples == len(combinations_list):
combinations_random_chosen = combinations_list
else:
combinations_random_chosen = []
random_combinations_index = np.random.choice(range(0, len(combinations_list)), n_samples, replace=False)
combinations_random_chosen = [combinations_list[x] for x in random_combinations_index]
# Pull out the X and Y to plot
rand_y, rand_x = [x[0] for x in combinations_random_chosen], [x[1] for x in combinations_random_chosen]
# Plot
plt.clf()
plt.scatter(rand_y, rand_x, c=['blue']*len(combinations_random_chosen))
plt.gca().set(xlabel='learn_rate', ylabel='min_samples_leaf', title='Random Search Hyperparameters')
plt.gca().set_xlim([0.01, 1.5])
plt.gca().set_ylim([10, 29])learn_rate_list = list(np.linspace(0.01, 1.5, 200))
# Create a list of values for the min_samples_leaf hyperparameter
min_samples_list = list(range(10, 30))
# Combination list
combinations_list = [list(x) for x in product(learn_rate_list, min_samples_list)]
# Confirm how many hyperparameter combinations & print
number_combs = len(combinations_list)
print(number_combs)
# Sample and visualize specified combinations
sample_and_visualize_hyperparameters(50)4000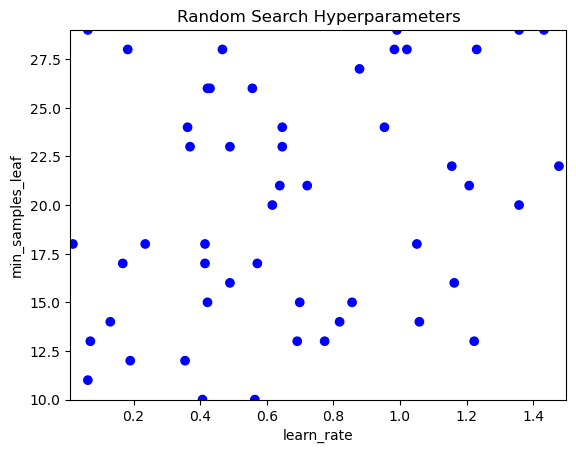
Just like the GridSearchCV library from Scikit Learn, RandomizedSearchCV provides many useful features to assist with efficiently undertaking a random search. You’re going to create a RandomizedSearchCV object, making the small adjustment needed from the GridSearchCV object.
The desired options are:
from sklearn.model_selection import train_test_split
credit_card = pd.read_csv('dataset/credit-card-full.csv')
# To change categorical variable with dummy variables
credit_card = pd.get_dummies(credit_card, columns=['SEX', 'EDUCATION', 'MARRIAGE'], drop_first=True)
X = credit_card.drop(['ID', 'default payment next month'], axis=1)
y = credit_card['default payment next month']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, shuffle=True)from sklearn.ensemble import GradientBoostingClassifier
from sklearn.model_selection import RandomizedSearchCV
# Create the parameter grid
param_grid = {'learning_rate': np.linspace(0.1, 2, 150),
'min_samples_leaf': list(range(20, 65))}
# Create a random search object
random_GBM_class = RandomizedSearchCV(
estimator=GradientBoostingClassifier(),
param_distributions=param_grid,
n_iter=10,
scoring='accuracy', n_jobs=4, cv=5, refit=True, return_train_score=True
)
# Fit to the training data
random_GBM_class.fit(X_train, y_train)
# Print the values used for both hyperparameters
print(random_GBM_class.cv_results_['param_learning_rate'])
print(random_GBM_class.cv_results_['param_min_samples_leaf'])[0.9416107382550335 0.7375838926174496 1.719463087248322
0.7885906040268456 1.8469798657718122 1.6684563758389261
0.3932885906040269 0.22751677852348992 0.7248322147651006
0.11275167785234899]
[20 46 37 47 28 26 51 35 57 48]Let’s practice building a RandomizedSearchCV object using Scikit Learn.
The hyperparameter grid should be for max_depth (all values between and including 5 and 25) and max_features (‘auto’ and ‘sqrt’).
The desired options for the RandomizedSearchCV object are:
from sklearn.ensemble import RandomForestClassifier
# Create the parameter grid
param_grid = {'max_depth': list(range(5, 26)), 'max_features': ['auto', 'sqrt']}
# Create a random search object
random_rf_class = RandomizedSearchCV(
estimator=RandomForestClassifier(n_estimators=80),
param_distributions=param_grid, n_iter=5,
scoring='roc_auc', n_jobs=4, cv=3, refit=True, return_train_score=True
)
# Fit to the training data
random_rf_class.fit(X_train, y_train)
# Print the values used for both hyperparameters
print(random_rf_class.cv_results_['param_max_depth'])
print(random_rf_class.cv_results_['param_max_features'])/Users/kakamana/opt/anaconda3/lib/python3.9/site-packages/sklearn/ensemble/_forest.py:424: FutureWarning: `max_features='auto'` has been deprecated in 1.1 and will be removed in 1.3. To keep the past behaviour, explicitly set `max_features='sqrt'` or remove this parameter as it is also the default value for RandomForestClassifiers and ExtraTreesClassifiers.
warn(
/Users/kakamana/opt/anaconda3/lib/python3.9/site-packages/sklearn/ensemble/_forest.py:424: FutureWarning: `max_features='auto'` has been deprecated in 1.1 and will be removed in 1.3. To keep the past behaviour, explicitly set `max_features='sqrt'` or remove this parameter as it is also the default value for RandomForestClassifiers and ExtraTreesClassifiers.
warn(
/Users/kakamana/opt/anaconda3/lib/python3.9/site-packages/sklearn/ensemble/_forest.py:424: FutureWarning: `max_features='auto'` has been deprecated in 1.1 and will be removed in 1.3. To keep the past behaviour, explicitly set `max_features='sqrt'` or remove this parameter as it is also the default value for RandomForestClassifiers and ExtraTreesClassifiers.
warn([23 15 23 5 8]
['sqrt' 'sqrt' 'auto' 'sqrt' 'sqrt']
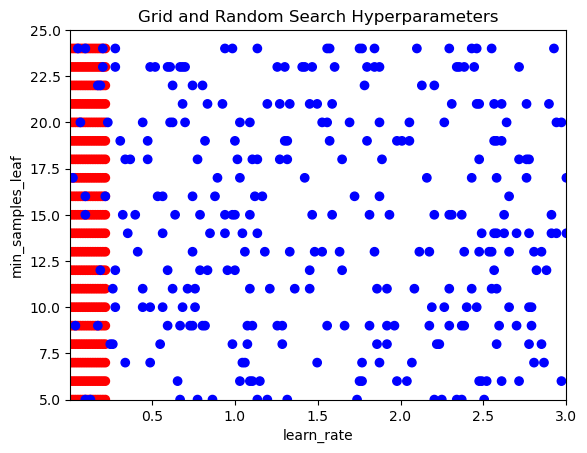
Visualizing the search space of random and grid search together allows you to easily see the coverage that each technique has and therefore brings to life their specific advantages and disadvantages.
In this exercise, you will sample hyperparameter combinations in a grid search way as well as a random search way, then plot these to see the difference.
def visualize_search(grid_combinations_chosen, random_combinations_chosen):
grid_y, grid_x = [x[0] for x in grid_combinations_chosen], [x[1] for x in grid_combinations_chosen]
rand_y, rand_x = [x[0] for x in random_combinations_chosen], [x[1] for x in random_combinations_chosen]
# Plot all together
plt.scatter(grid_y + rand_y, grid_x + rand_x, c=['red']*300 + ['blue']*300)
plt.gca().set(xlabel='learn_rate', ylabel='min_samples_leaf', title='Grid and Random Search Hyperparameters')
plt.gca().set_xlim([0.01, 3.0])
plt.gca().set_ylim([5, 25])learn_rate_list = np.linspace(0.01, 3.0, 200)
min_samples_leaf_list = range(5, 25)
combinations_list = [list(x) for x in product(learn_rate_list, min_samples_leaf_list)]
# Sample grid coordinates
grid_combinations_chosen = combinations_list[0:300]
# Create a list of sample indexes
sample_indexes = list(range(0, len(combinations_list)))
# Randomly sample 300 indexes
random_indexes = np.random.choice(sample_indexes, 300, replace=False)
# Use indexes to create random sample
random_combinations_chosen = [combinations_list[index] for index in random_indexes]
# Call the function to produce the visualization
visualize_search(grid_combinations_chosen, random_combinations_chosen)